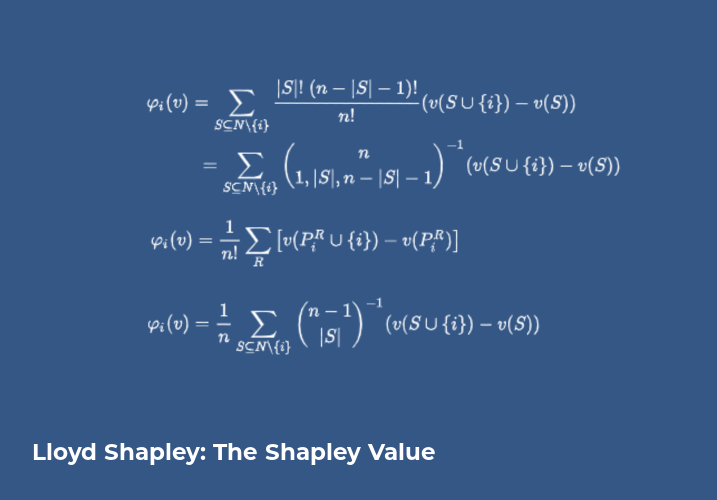The Work

See Below for Definitions, “Evolution - 8 Steps” pdf, Bibliography, More Resources

1 - OUTCOMES AS COALITIONS (THE SHAPLEY VALUE)

An n-person game consists of n players competing to obtain a total utility payoff. The Shapley Value enables identification of possible outcomes in the form of coalitions whose members cooperate to share in the total utility payoff. Cooperation consists of side payments of utility among the players as an incentive to get the players to join or to quit coalitions. The Shapley Value of a player allocates the total payoff of the game among coalition members, when the player cooperates and joins a coalition. This value determines the side payment, if any, to the joining players. Multiple outcomes with different groups of coalitions may form based on the allocation of total payoff and the side payments.

The definition of coalitions and the benefits to cooperation represented by the Shapley Value are the keystone of the n-person game theory work by Lloyd Shapley. The Shapley Value has been used for coalition/outcome analysis on a wide range of applications, including favoritism, tax policy, control and power among stockholders of a corporation, power and stability in politics, aircraft landing fees, and cost allocation for the TN Valley Authority.

2 - DEFERRED ACCEPTANCE (GALE, ShAPLEY MATCHING) aka The MARRIAGE  PROBLEM

A large set of people seek access to a limited number of available options from a small number of providers of those options. Providers of the options must decide which of the seeking persons shall be awarded access to their available options. Seekers state preferences regarding the options. Providers have preferences regarding the seekers who desire access to their options. The deferred matching algorithm continually varies the matches between seekers and options according to the preferences of each provider for the seeker.

In each cycle of the algorithm, every remaining seeker points to the option preferred most among the remaining options. Every remaining provider points to the remaining seeker who has the highest priority for that provider. As each additional seeker is considered, another seeker may be unmatched to satisfy the higher preferences for the new seeker under consideration. Unmatched persons will have to be reconsidered later in the matching process. Final matching decisions are deferred until all of the available options have been committed to a seeker and no further improvements can be made. Seekers obtain the best results from this matching process by truthful reporting of preferences.

This matching algorithm guarantees that the people seeking and the providers cannot obtain a better result.

“College Admissions and the Stability of Marriage” was the title of Gale and Shapley’s 1962 paper, but their algorithm has been employed over a wide range of situations. Examples include matching college applicants (people seeking) to limited university (providers) admissions slots (options) and matching medical school graduates (people seeking) to resident programs (options) at hospitals (providers).

3 - LLOYD, WHAT ARe YOU THINKING? (VALUES OF N PERSON GAMES) 

This example takes you directly into the mind of Lloyd Shapley as he reasons about the solutions to a game with multiple players. In this table, Lloyd Shapley demonstrates the use of inductive logic to derive his equation for the general n-person game. Inductive logic reasons from specific to general. This table begins by deriving the value to each player in a 3-person constant sum game which is a very specific game. At the end of the table, the value to each player is given for a 3-person general sum game, which is a more general game. Ultimately, these characterizations would lead to the specification of the value to each player in a general n-person game – the Shapley value described above.

5 - WHO REALLY WINS (CORES AND BALANCED SETS) 

Different coalition memberships may produce multiple outcomes that can win or “solve” the game. The Shapley value provides those possible outcomes. The core of the game is those outcomes that cannot be improved upon by any coalition and cannot be blocked by any coalition.  Outcomes that can actually win the game appear in the core. Outcomes in the core are those outcomes (based on Shapley values) in which the players would not be better off by playing alone or by switching coalitions.  

In some games, the core is empty. A core will be empty if some of the players in possible outcomes would be better off by playing alone or by switching coalitions. Possible outcomes may result in coalitions in which players are better off forming smaller coalitions and simply sharing the total payoff of the game. The set of possible outcomes which are better off forming smaller coalitions is called the stable set. Typically, the stable set contains more possible outcomes than the core and is more likely to lead to solutions than the more restrictive conditions for inclusion in the core solution.

A common and important application of the core is identifying competitive prices for winning coalitions in commodity trading markets. Another common application of the core has been to find competitive prices for winning prices in the real-estate housing market. 

6 - A MAJORITY WINS (SHAPLeY - SHUBIK POWER INDEX) 

A simple game is one in which players/coalitions either win or lose the total payoff.  For these games, Lloyd Shapley and Martin Shubik collaborated to identify a modified version of the Shapley Value. The foundation for this method is to identify pivot players. A pivot player is one who will cause a coalition to transition from losing to winning if the player joins the coalition or vice-versa. All other players cannot affect the outcome and are called dummy players. Pivot players have all the control and are given a share of the payoff in determining the outcome of the game. Dummy players have no value and do not impact the outcomes of the game.

The Shapley-Shubik power index has the greatest application in games where a majority wins. In their initial 1954 paper, Shapley and Shubik applied the indexing method to decision-making in a committee. Other applications have included the Electoral College in US presidential elections, limits imposed on small parties in Italy and shareholder control of corporations and corporate buyouts.

8 - A ROLL OF THE DICE (STOCHASTIC GAMES)

Two players are attempting to control an environment. This environment exists in one of several states. As play proceeds, the players make decisions that alter the state of the environment. One player receives a payoff from the other player. The game may continue or terminate after each play. A maximum total payoff may be earned over the life of the game. State changes in the environment, payoff transfers and continuation/termination decisions at each play are controlled by probabilities. These probabilities change as play proceeds.

At each play of the game, the player faces a contradiction. Payoff from his decision contributes to his current total payoff but may result in termination of the game. As a result, the player may accrue a smaller total payoff despite maximizing the payoff for each play of the game until termination.

A solution for this type of game consists of a strategy that provides a decision for each player at every possible play of the game for every possible history of decisions.  Shapley proved that such a solution exists. Continues in Evolution…8 Steps…pdf

COMPLETE SUMMARIES & BIBLIOGRAPHY

Evolution of Lloyd Shapley Game Theory - 8 Steps (Krell) [PDF]
Bibliography - First Publication of Shapley’s 8 Steps (Krell) [PDF]

More Resources

Alvin E Roth, Ed. “Handbook of the Shapley Value,” Chapman & Hall/CRC Series in Operations Research. Brief chapter summaries are at https://www.tandfonline.com/doi/full/10.1080/00401706.2020.1744904 .

American Mathematical Society Feature Column Theoretical Mathematics Finds Use in Economics--A Tribute to Lloyd Shapley

Back to Summaries ↑

Game theory Definitions

n players: An arbitrary number of players in a game.

utility:  Benefit to each player for participating in the game.

Utility may be in the form of relative preference, costs, product or any commodity that might be shared among the players.

transferable utility: Utility in a form that can be transferred from one player to another player.

payoff: The amount of utility paid to each player before starting the game.

total payoff: The total utility paid to all the players for participating before starting the game.

cooperation: Exchange of utility among the players with the goal of winning the game.

coalition: A group of players who combine their utility to obtain the best payoff for players in the group.

outcome: A set of coalitions that allocates total payoff to the players in each coalition.

Coalition members share the total payoff of the game as a result of cooperation.

winning: The outcome that leaves every coalition with the “best” allocation of total utility.

Back to Summaries ↑

LLOYD | The Work | The Game | STORIES | THE PRIZES